[Focus on] Cybersecurity Research activities of the CAS³C³ Team of Laboratoire Jean Kuntzmann

Cybersecurity research activities of the CAS³C³ team (computer algebra, security, complex systems, codes, secrets, cryptology) are focused on

  • Design and analysis of symmetric cryptographic primitives and their secure and efficient implementation.
  • Proof of work certificates for outsourced cloud computing.
  • Fault tolerant schemes in linear algebra.
  • Secure protocols for multi-party, zero-knowledge or industrial control systems.

Proof of work certificates for outsourced cloud computing, where a client can not blindly trust the answer of remote computing parties

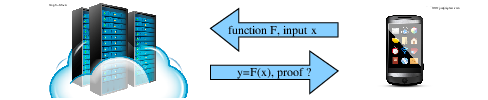Efficiently and reliably delegating computations. The idea is to design algorithms that can form a proof of correctness of a result computed via a probabilistic algorithm or through a potentially unreliable computing center. The difficulty is to design proofs that are verifiable at a lower cost (time, memory, …) than that of recomputing the result.

References: hal-02191075 hal-01829139 hal-01825779 hal-01657873 hal-01503870 hal-01466093 hal-01266041 hal-00932846

Explicit computation of (freestart) collisions for the SHA-1 hash function

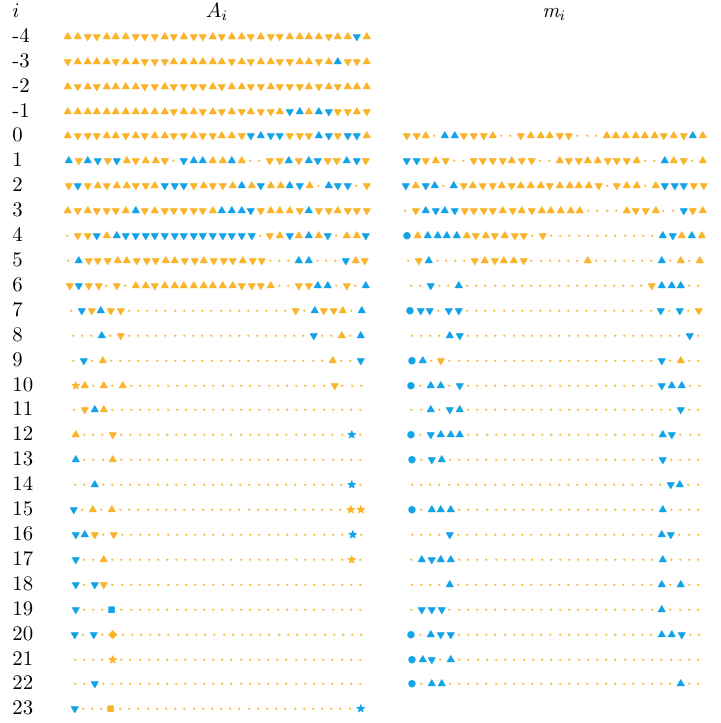Signed non-linear differential path used in the computation of the second block of a collision for the SHA-1 hash function.

Hash functions, of which SHA-1 is an example, are ubiquitous primitives in cryptography. It was known since 2005 that SHA-1 was vulnerable to collision attacks, yet it remained used in many industrial products. From 2014 to 2017, a series of work involving CASC team member Pierre Karpman improved the existing attacks and ultimately lead to an explicit computation of a collision for SHA-1. This had a positive impact on the withdrawal of this function from vulnerable systems.

References: hal-01982005 hal-01251023

Fault tolerant schemes for linear algebra

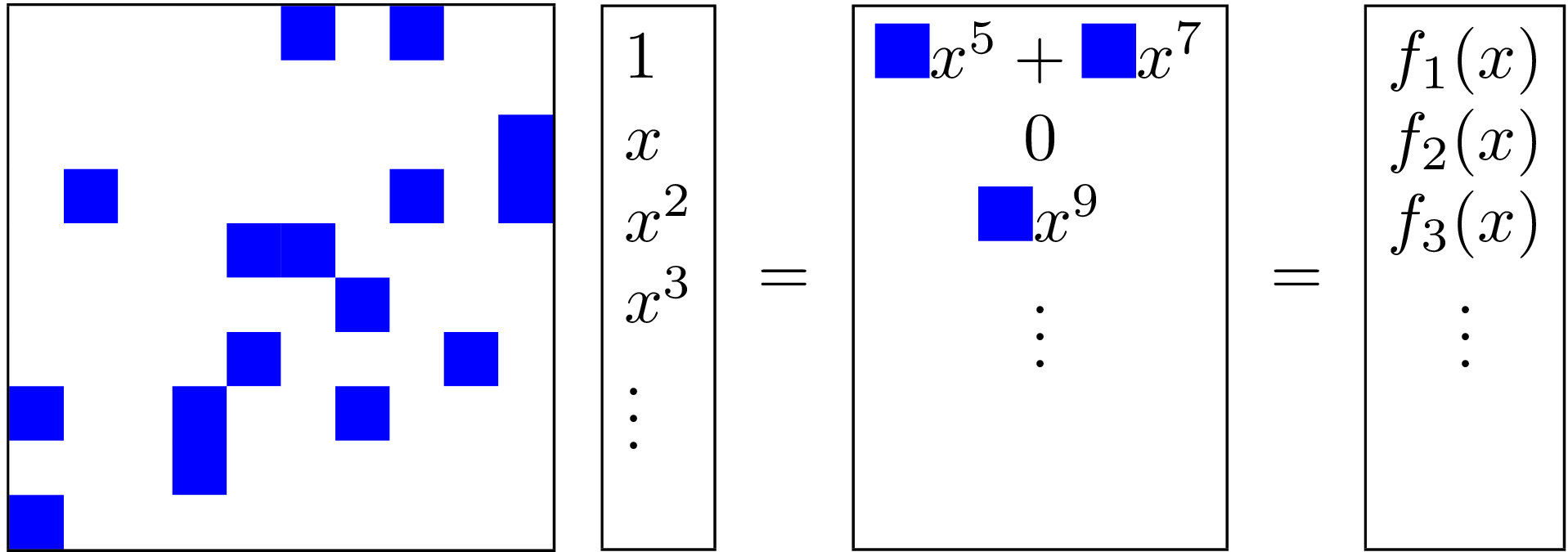Solving linear systems of parametric equations: hal-01982114
Error correction in fast exact linear algebra: Error correction in fast matrix multiplication and inverse arXiv:1802.02270, Factorization with errors: hal-01997592

Information retrievability, proofs and security

high-order masking schemes for finite-field multiplication

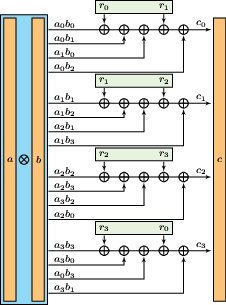A 3-NI multiplication gadget over F2 and any extension thereof.

Physical side-channel attacks are a significant threat for embedded implementations of cryptosystems. An efficient countermeasure against some of these attacks is the use of masked operations, whereby one splits sensitive data into several shares and uses multiparty computation secure in a probing model to compute a shared result. Team members’ activities include the study of efficient algorithms to evaluate the security of given masking schemes, and the design of new gadgets for various operations.

References: hal-01878385

Zero-knowledge protocols

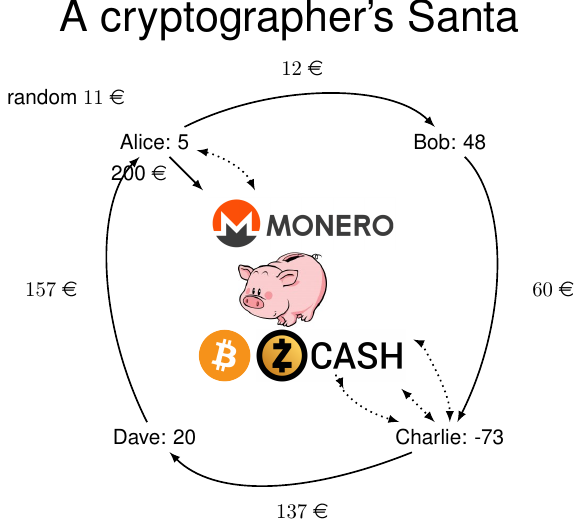In Conspiracy Santa, a variant of Secret Santa, a group of people offer each other Christmas gifts, where each member of the group receives a gift from the other members of the group. We have invented a protocol that allows a group of people to share the expenses for the gifts in such a way that no participant will learn the price of his gift. Our solution does not require a trusted third party, and can either be implemented physically (the participants are in the same room and exchange money) or, virtually, using a cryptocurrency.

More generally, we research on Physical Cryptography, the art of designing protocols that can be ran without computers, for instance using only pencil and paper or cards.

Private Multi-party linear algebra and trust computation

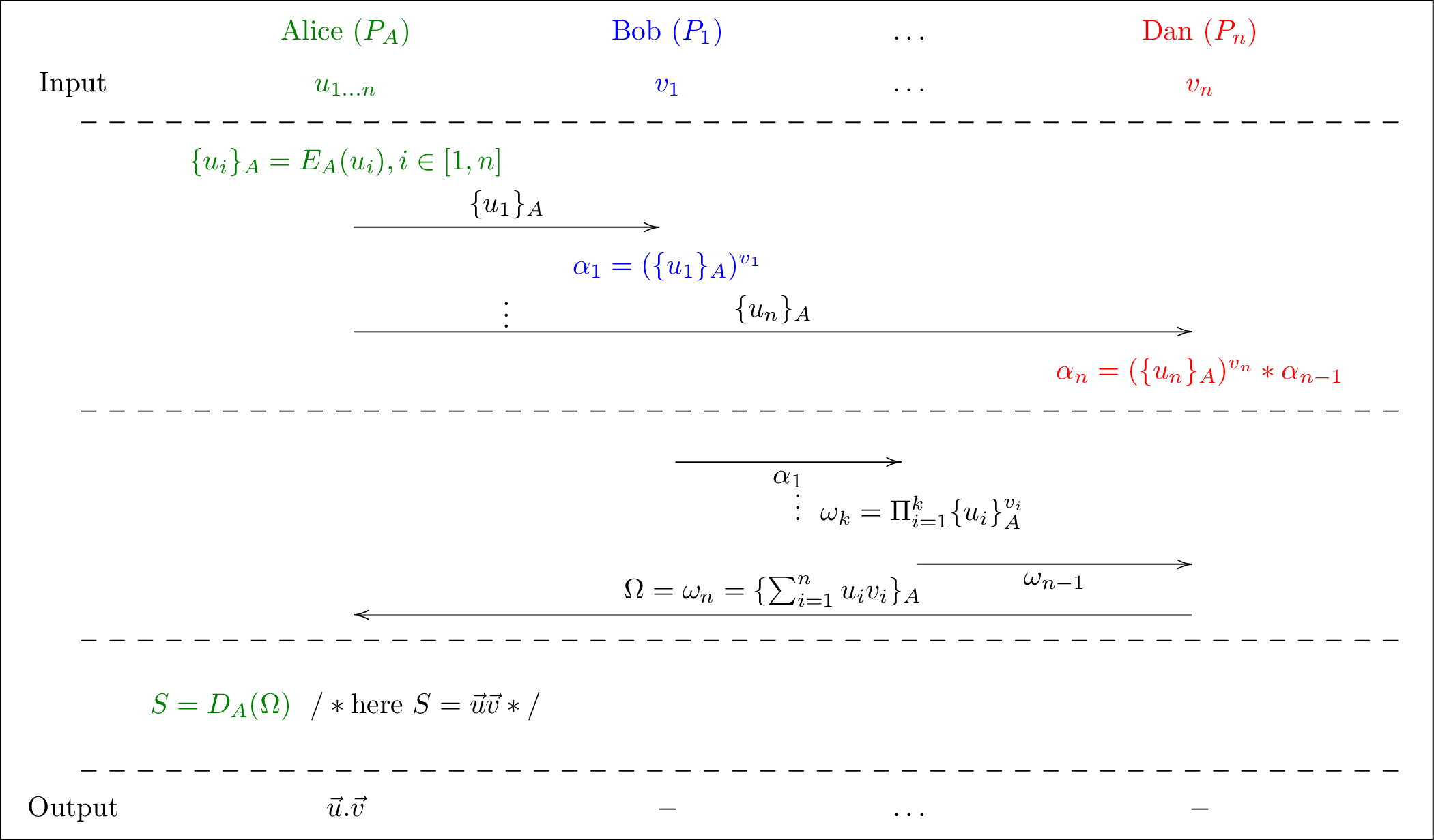Secure multiparty computations (MPC) allows n players to compute together the output of some function, using private inputs without revealing them. This is useful, e.g., for a distributed evaluation of trust where players compute a confidence level by combining their mutual degrees of trust, but without revealing their personal measures.

References: hal-01781554 hal-01497866 hal-01344750 hal-00607478

Security architectures for industrial control systems

LocalPKI: A user-centric, interoperable and IoT friendly, formally proven PKI. This security infrastructure can use blockchain technologies and be used in constrained environments, for instance for IoT, but also for Supervisory Control and Data Acquisition (SCADA) architectures.

LocalPKI: hal-01963269 hal-01564696
Blockchains: hal-01874854 hal-02639358
Secured Industrial control systems: hal-01657605