[Focus on] Complex Systems Research activities
Complex systems research activities of the CAS³C³ team are focused on
- Discrete dynamical systems.
- Parallel graph rewriting and Graph transformations.
- Graph models for biology and astrophysics.
DEM-Systems
DEM-systems are a class of discrete dynamical systems with properties of
both cellular automata and L-systems. They are defined as sequences on a
one-dimensional loop with rules governing dynamics in which new sites
can be created, depending on the states of a neighbourhood of sites, and
complex behaviour can be generated. Unlike for CA, finite initial
sequences can produce positive spatial entropy over time.
However, even in cases where the entropy is zero, considerable
complexity is possible, especially when the sequence length grows to
infinity, and we demonstrate and study behaviours of DEM-systems
including fragmentation of sequences, self-reproducing patterns,
self-similar but irregular patterns, patterns that not only produce new
sites but produce producers of new sites, and sequences whose growth
rate is sublinear, linear, quadratic, cubic, or exponential.
Références: hal-00961656 hal-00953772 hal-01326782
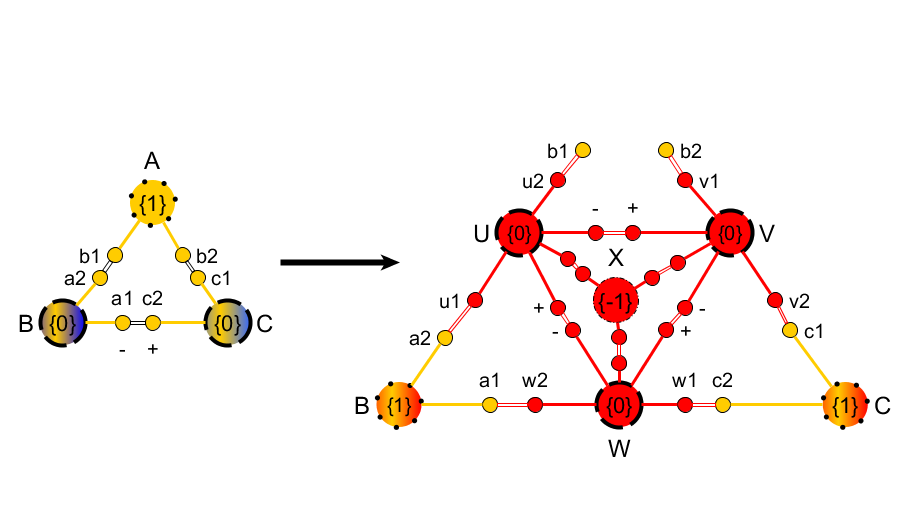
Parallel graph rewriting with overlapping rules
Considering an initial graph g and a system of rewriting rules R={l~i~
-> r~i~, i=1... n}, we rewrite the graph g into a graph g' by using,
simultaneously, the rules of R whose left-hand sides, l~i~, match
subgraphs of g. All the occurrences of the l~i~ in g are replacing by an
instance of r~i~. In order to deal with match overlapping, we introduce
the notion of pregraphs and follow the rewriting modulo approach.
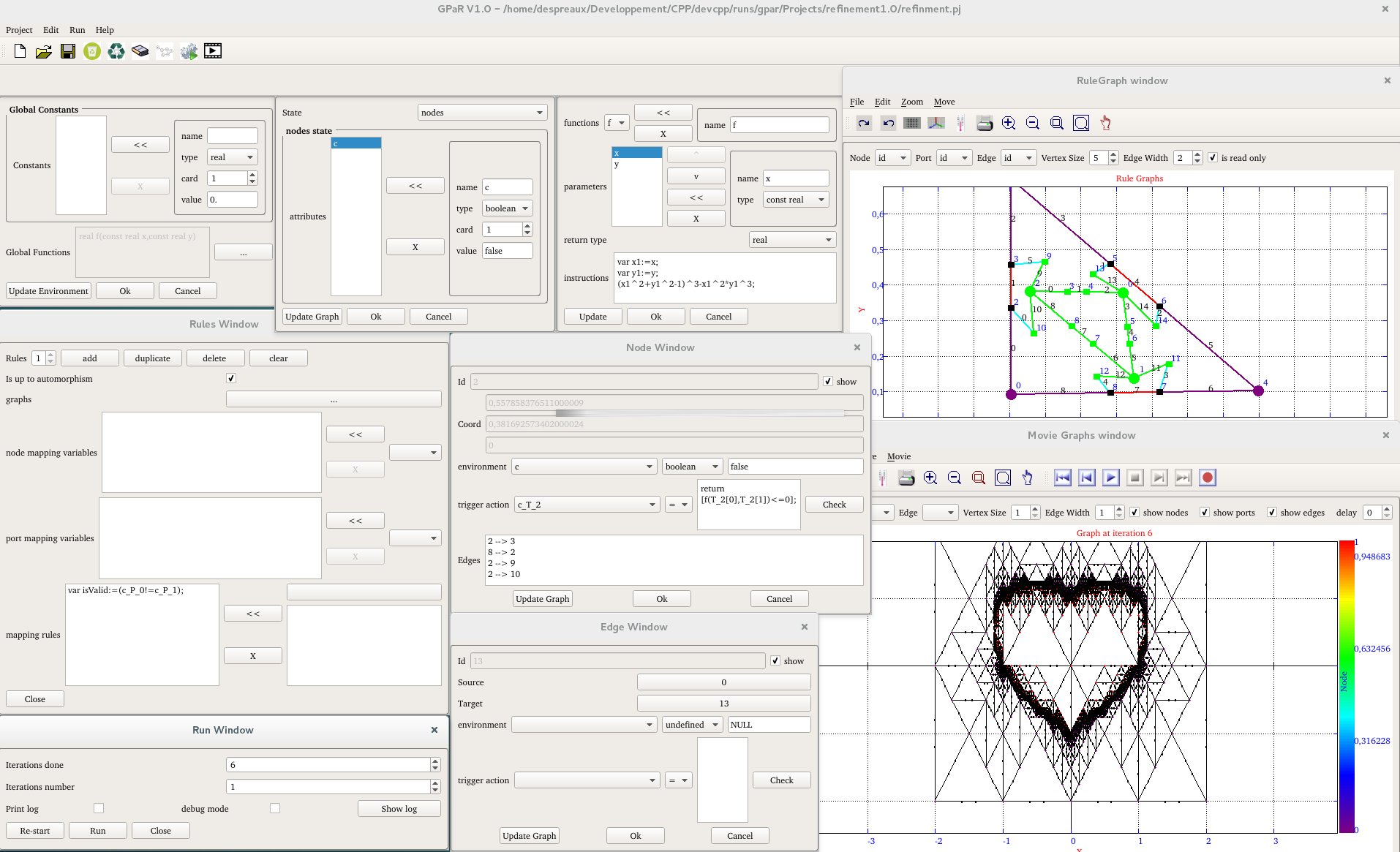GPaR is a parallel graph rewriting software implemented in C++ with a
graphical user interface. It can be used in a large variety of rewriting
problems including cellular automata, L-systems and fractal systems.
Références: hal-01408834 hal-02084261 hal-01985043 hal-01898363
Split thickness of graphs
We examine the planar split thickness of a graph, that is, the smallest
k such that the graph is k-splittable into a planar graph. A k-split
operation substitutes a vertex v by at most k new vertices such that
each neighbor of v is connected to at least one of the new vertices.
Simulating aggregates of bivalents in 2n=40 mouse meiotic spermatocytes through inhomogeneous percolation processes
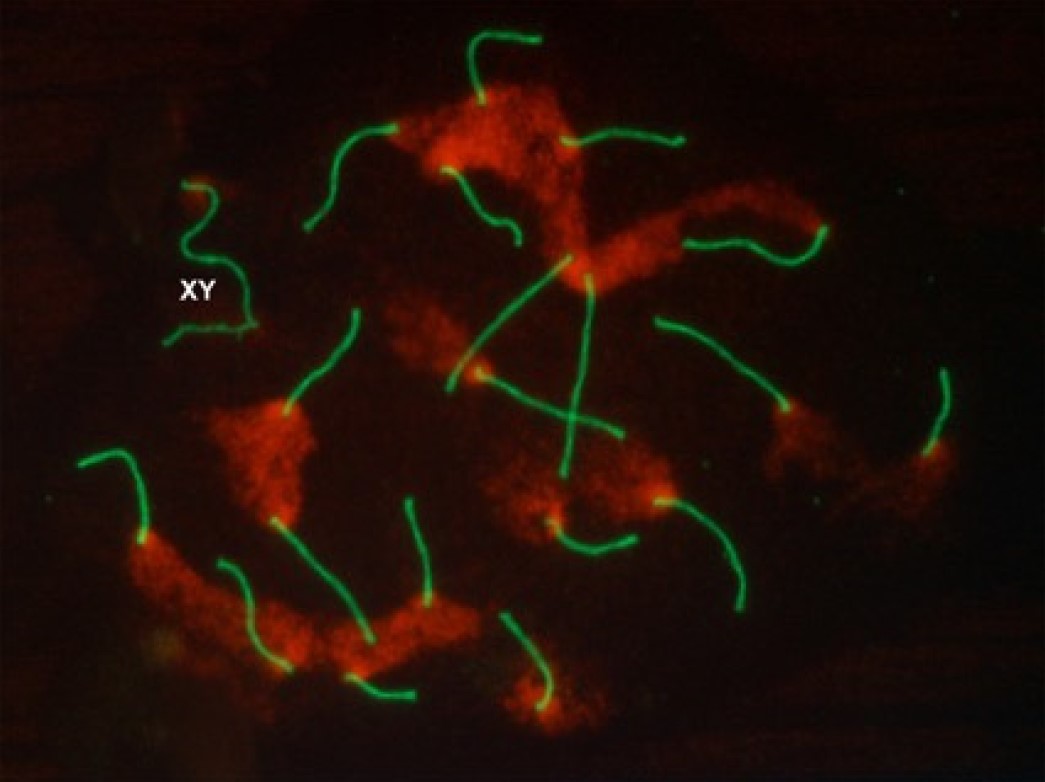
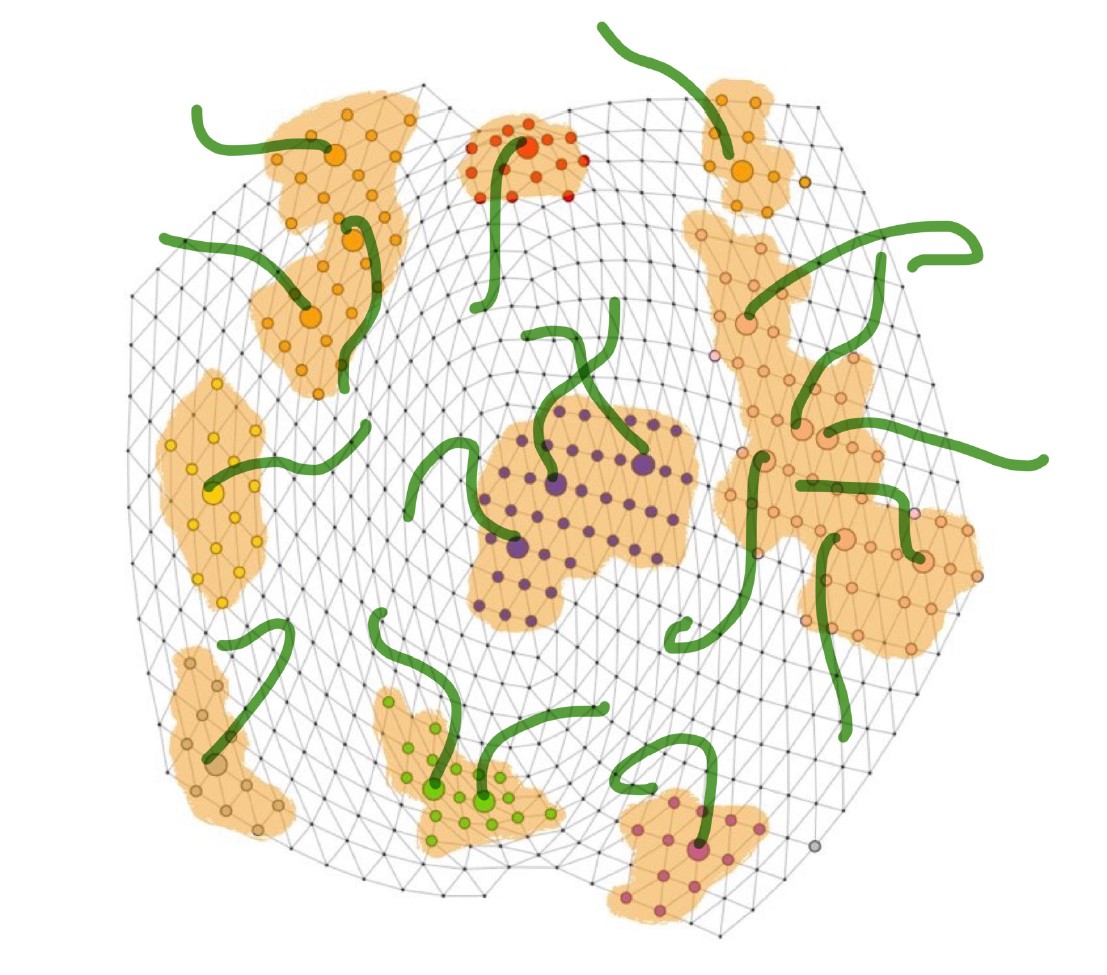We show that an inhomogeneous Bernoulli site percolation process running
upon a fullerene's dual C'~1200~ can be used for representing
bivalents attached to the nuclear envelope in mouse Mus M. Domesticus
2n=40 meiotic spermatocytes during pachytene. It is shown that the
induced clustering generated by overlapping percolation domains
correctly reproduces the probability distribution observed in the
experiments (data) after fine tuning the parameters.
Références: hal-01823737 hal-01814944 hal-01982363
Simulation of hierarchical n-body systems based on dynamical trees
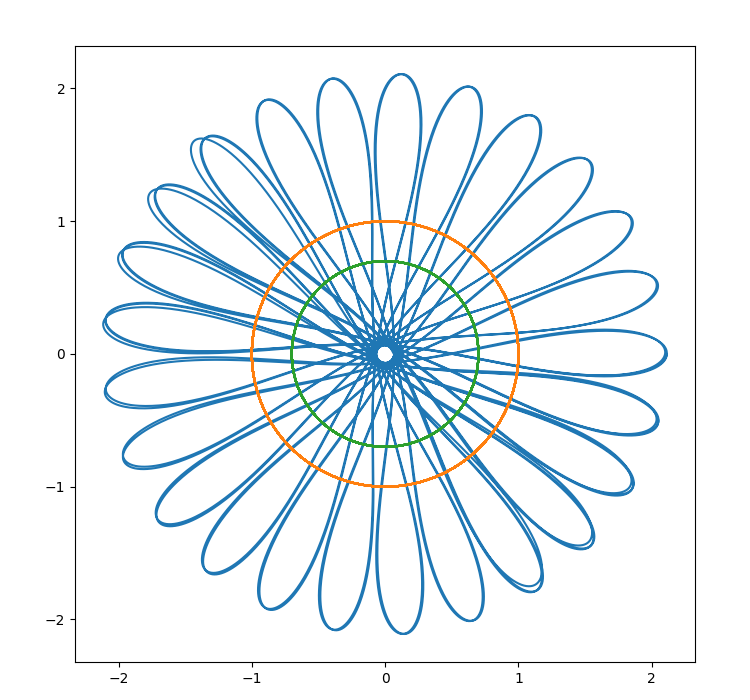We present an algorithm to simulate the gravitational interaction of a
large number of point masses. This problem is known as the n-body
problem in physics and astronomy. The algorithm detects and uses
hierarchical structure present in the current state of the point masses
to speed up the computation. The structure is represented as a dynamical
tree.
Références: hal-00769677